预测模块工作过程:
预测模块根据输入的地图数据,以及传感器融合的数据,生成并输出一些预测数据,
这些预测数据,包含了周围所有其他机动车以及其他移动物体的未来状态。
通常,这些预测数据可以展示为若干可能的运动轨迹。
预测数据还包括每条轨迹的几率大小;
预测技术常用有两种:
1.基于模型法
使用运动数学模型,预测运动轨迹,
2.数据驱动法
依赖于机器学习和案例学习
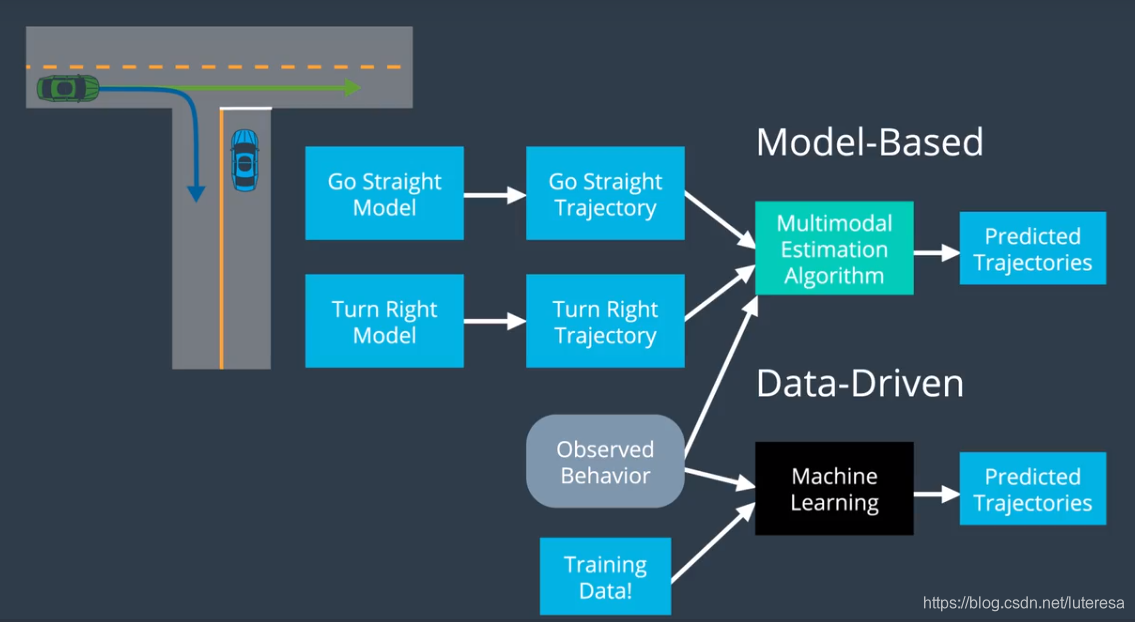
基于模型方法吸收了有关物理限制的知识(来自道路交通状况等),而机器学习可以根据大量历史数据来学习。
1.数据驱动法
一般分两个阶段:
第一阶段,离线训练阶段,,算法从数据中学习模式;
用轨迹聚合算法
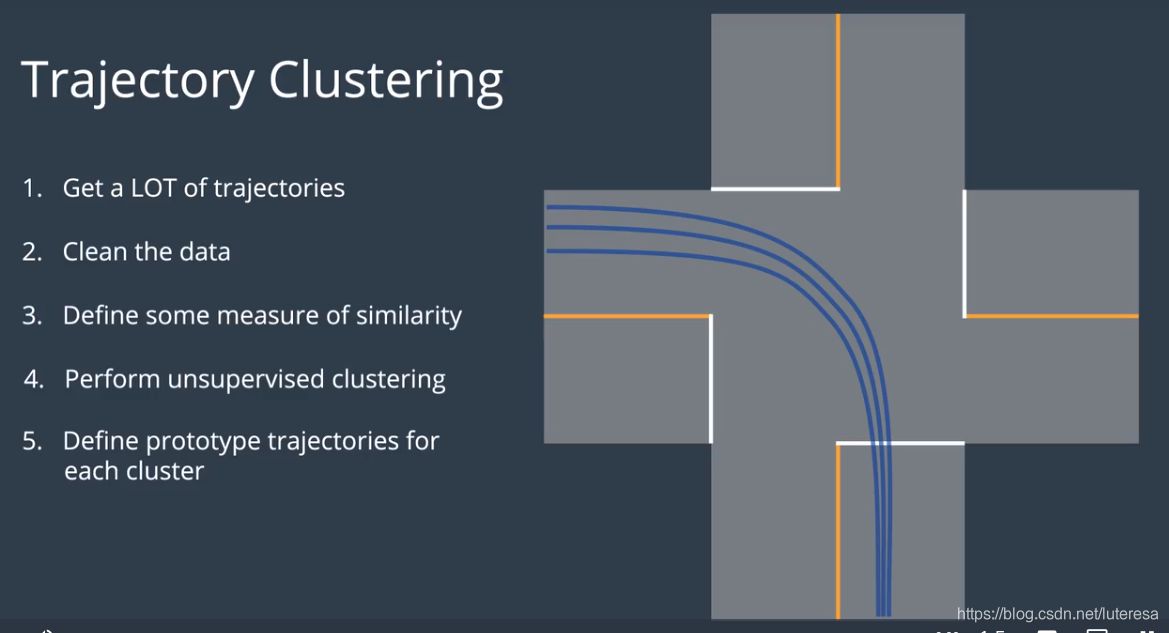
第二阶段,在线预测阶段,算法使用模型来预测;
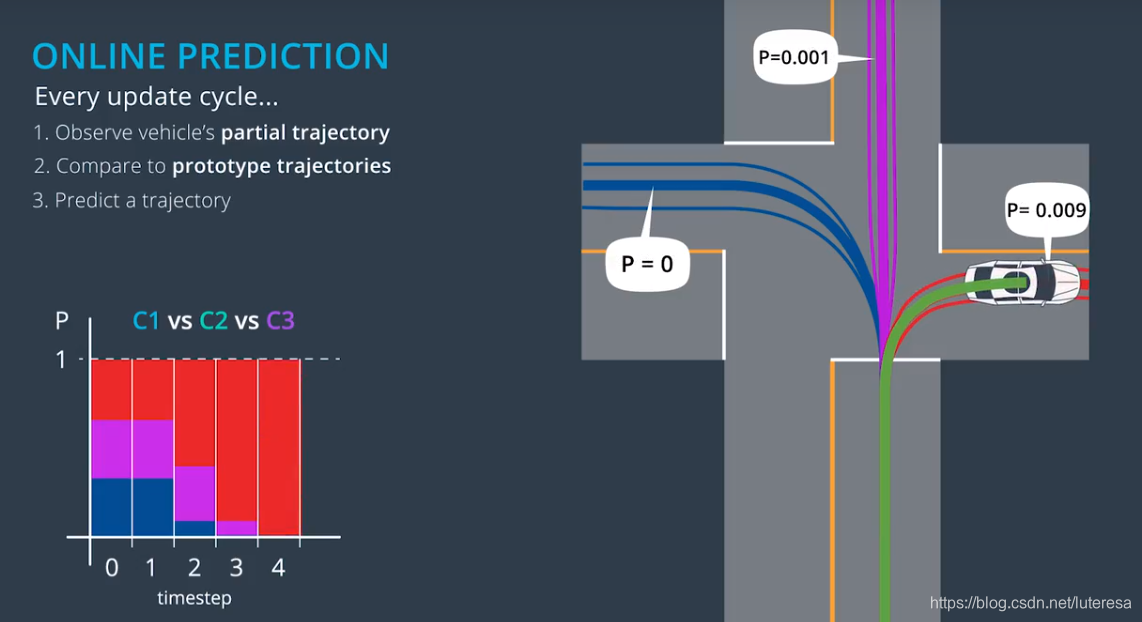
2. 基于模型法
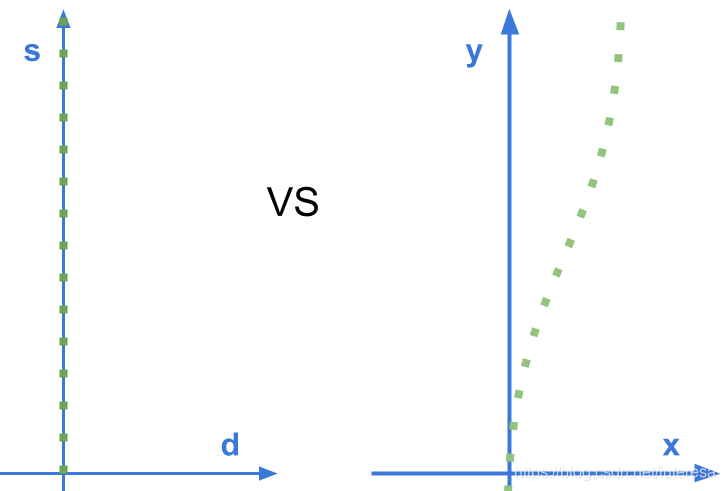
2.1Frenet Coordinates
以无人车为原点,横向位移为d,纵向位移为s
The Paper
You can find the paper here: A comparative study of multiple-model algorithms for maneuvering target tracking
辅助材料
A comparative study of multiple-model algorithms for maneuvering target tracking
2.2 Defining Process Models
You saw how process models can vary in complexity from very simple...
$$
\begin{bmatrix} \dot{s}\ \dot{d} \end{bmatrix}=\begin{bmatrix} s_{0} \ 0 \end{bmatrix} + {w}
$$
to very complex...
$$
\begin{bmatrix} \ddot{s} \ \ddot{d} \ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{\theta}\dot{d} + as \ -\dot{\theta}\dot{s} + \frac{2}{m}(F{c,f}\cos\delta + F_{c,r}) \ \frac{2}{I_z} (lf F{c,f} - lrF{c,r}) \end{bmatrix} + {w}
$$
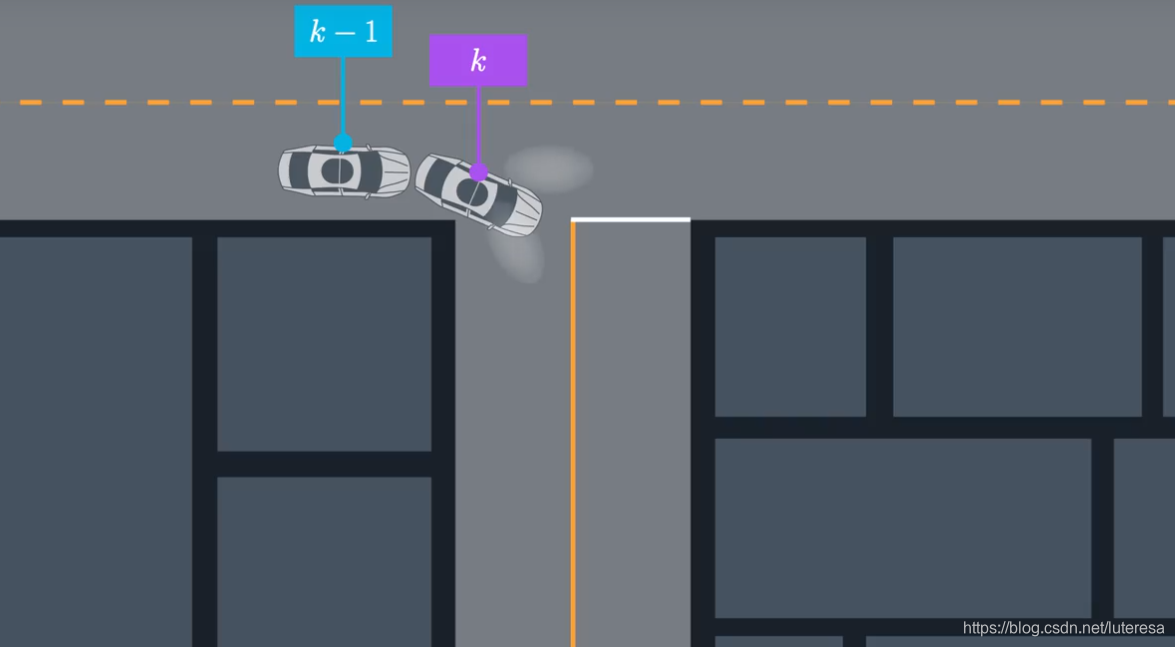
2.2 Using process models to compare driver behavior to what would be expected for each model.

2.3 Classifying Intent with Multiple Model Algorithm

两种方法的对比

实践中,最好的预测方法通常是某种混合方法,结合以上两种方法的长处,
在行为分类的混合法中,经常使用的一个策略是,把分类器和过滤器相结合,

C++实现朴素贝叶斯
预测轨迹类别:
1.change lanes left (shown in blue)
2.keep lane (shown in black)
3.or change lanes right (shown in red)
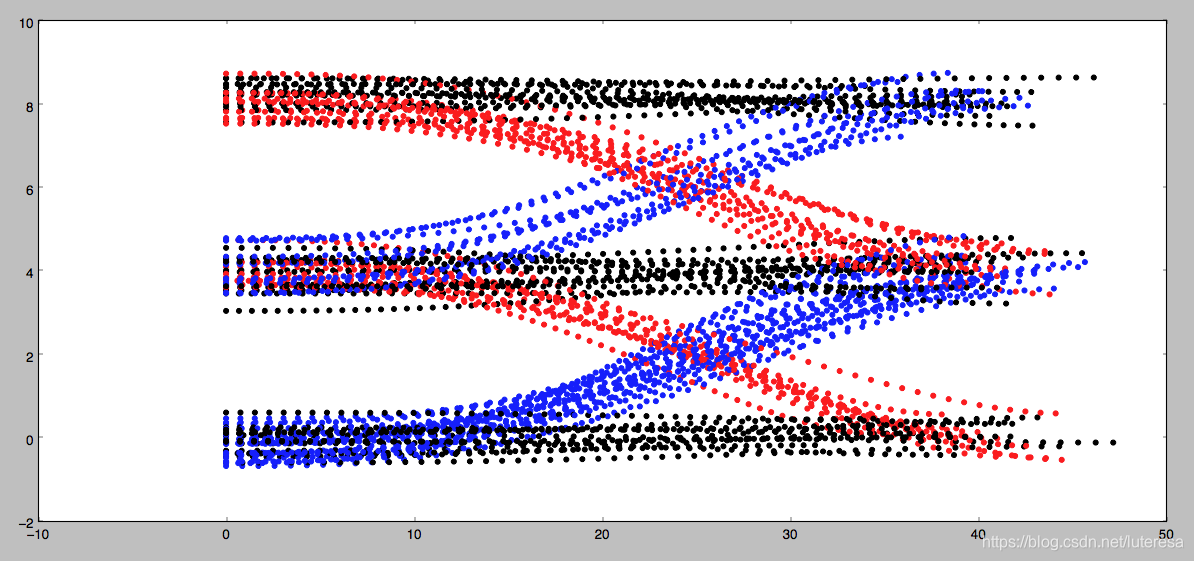
Each coordinate contains 4 features:
s
d
$\dot{s}$
$\dot{d}$
Instructions
1.Implement the train(data, labels) method in the class GNB in classifier.cpp.
Training a Gaussian Naive Bayes classifier consists of computing and storing the mean and standard deviation from the data for each label/feature pair. For example, given the label "change lanes left” and the feature $\dot{s}$
, it would be necessary to compute and store the mean and standard deviation of $\dot{s} $
over all data points with the "change lanes left” label.
Additionally, it will be convenient in this step to compute and store the prior probability p(C_k) for each label C_k. This can be done by keeping track of the number of times each label appears in the training data.
2.Implement the predict(observation) method in classifier.cpp.

Helpful Resources
sklearn documentation on GaussianNB
Wikipedia article on Naive Bayes / GNB
代码实现:
#include "classifier.h"
#include <math.h>
#include <string>
#include <vector>
using Eigen::ArrayXd;
using std::string;
using std::vector;
// Initializes GNB
GNB::GNB() {
/**
* TODO: Initialize GNB, if necessary. May depend on your implementation.
*/
left_means = ArrayXd(4);
left_means << 0,0,0,0;
left_sds = ArrayXd(4);
left_sds << 0,0,0,0;
left_prior = 0;
keep_means = ArrayXd(4);
keep_means << 0,0,0,0;
keep_sds = ArrayXd(4);
keep_sds << 0,0,0,0;
keep_prior = 0;
right_means = ArrayXd(4);
right_means << 0,0,0,0;
right_sds = ArrayXd(4);
right_sds << 0,0,0,0;
right_prior = 0;
}
GNB::~GNB() {}
void GNB::train(const vector<vector<double>> &data,
const vector<string> &labels) {
/**
* Trains the classifier with N data points and labels.
* @param data - array of N observations
* - Each observation is a tuple with 4 values: s, d, s_dot and d_dot.
* - Example : [[3.5, 0.1, 5.9, -0.02],
* [8.0, -0.3, 3.0, 2.2],
* ...
* ]
* @param labels - array of N labels
* - Each label is one of "left", "keep", or "right".
*
* TODO: Implement the training function for your classifier.
*/
// For each label, compute ArrayXd of means, one for each data class
// (s, d, s_dot, d_dot).
// These will be used later to provide distributions for conditional
// probabilites.
// Means are stored in an ArrayXd of size 4.
float left_size = 0;
float keep_size = 0;
float right_size = 0;
// For each label, compute the numerators of the means for each class
// and the total number of data points given with that label.
for (int i=0; i<labels.size(); ++i) {
if (labels[i] == "left") {
// conversion of data[i] to ArrayXd
left_means += ArrayXd::Map(data[i].data(), data[i].size());
left_size += 1;
} else if (labels[i] == "keep") {
keep_means += ArrayXd::Map(data[i].data(), data[i].size());
keep_size += 1;
} else if (labels[i] == "right") {
right_means += ArrayXd::Map(data[i].data(), data[i].size());
right_size += 1;
}
}
// Compute the means. Each result is a ArrayXd of means
// (4 means, one for each class)
left_means = left_means/left_size;
keep_means = keep_means/keep_size;
right_means = right_means/right_size;
// Begin computation of standard deviations for each class/label combination.
ArrayXd data_point;
// Compute numerators of the standard deviations.
for (int i=0; i<labels.size(); ++i) {
data_point = ArrayXd::Map(data[i].data(), data[i].size());
if (labels[i] == "left"){
left_sds += (data_point - left_means)*(data_point - left_means);
} else if (labels[i] == "keep") {
keep_sds += (data_point - keep_means)*(data_point - keep_means);
} else if (labels[i] == "right") {
right_sds += (data_point - right_means)*(data_point - right_means);
}
}
// compute standard deviations
left_sds = (left_sds/left_size).sqrt();
keep_sds = (keep_sds/keep_size).sqrt();
right_sds = (right_sds/right_size).sqrt();
//Compute the probability of each label
left_prior = left_size/labels.size();
keep_prior = keep_size/labels.size();
right_prior = right_size/labels.size();
}
string GNB::predict(const vector<double> &sample) {
/**
* Once trained, this method is called and expected to return
* a predicted behavior for the given observation.
* @param observation - a 4 tuple with s, d, s_dot, d_dot.
* - Example: [3.5, 0.1, 8.5, -0.2]
* @output A label representing the best guess of the classifier. Can
* be one of "left", "keep" or "right".
*
* TODO: Complete this function to return your classifier's prediction
*/
// Calculate product of conditional probabilities for each label.
double left_p = 1.0;
double keep_p = 1.0;
double right_p = 1.0;
for (int i=0; i<4; ++i) {
left_p *= (1.0/sqrt(2.0 * M_PI * pow(left_sds[i], 2)))
* exp(-0.5*pow(sample[i] - left_means[i], 2)/pow(left_sds[i], 2));
keep_p *= (1.0/sqrt(2.0 * M_PI * pow(keep_sds[i], 2)))
* exp(-0.5*pow(sample[i] - keep_means[i], 2)/pow(keep_sds[i], 2));
right_p *= (1.0/sqrt(2.0 * M_PI * pow(right_sds[i], 2)))
* exp(-0.5*pow(sample[i] - right_means[i], 2)/pow(right_sds[i], 2));
}
// Multiply each by the prior
left_p *= left_prior;
keep_p *= keep_prior;
right_p *= right_prior;
double probs[3] = {left_p, keep_p, right_p};
double max = left_p;
double max_index = 0;
for (int i=1; i<3; ++i) {
if (probs[i] > max) {
max = probs[i];
max_index = i;
}
}
return this -> possible_labels[max_index];
}