1. 传感器
在无人驾驶系统中,对物体跟踪和预测,目前常用的传感器有Laser 和 Radar。
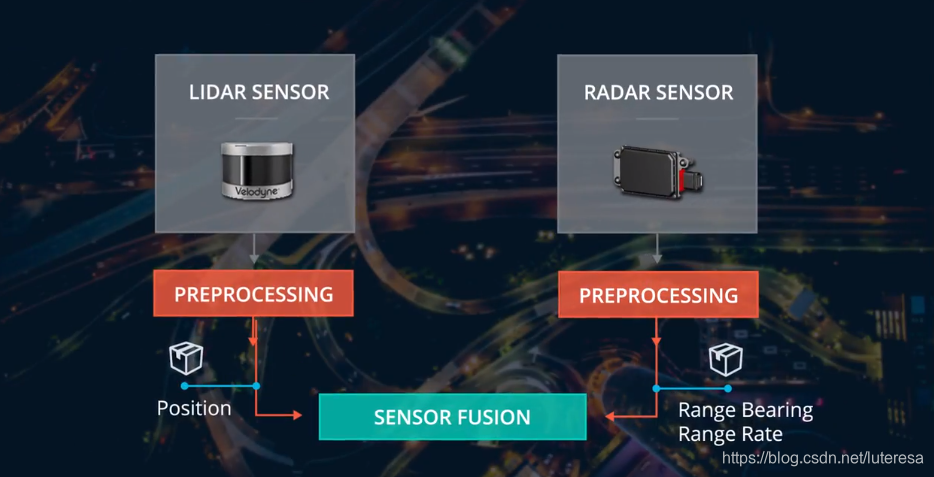
激光:可以测量准确的位置信息$P_x, P_y$,实际上无法直接观测其速度;
雷达:根据多普勒效应,雷达能直接测量移动对象的经向速度;
如果能够把激光和雷达的测量值都融合进卡尔曼滤波系统中,那么可以更好的改进跟踪系统,能够准确地估算行人位置、方向和速度。
2 传感器融合
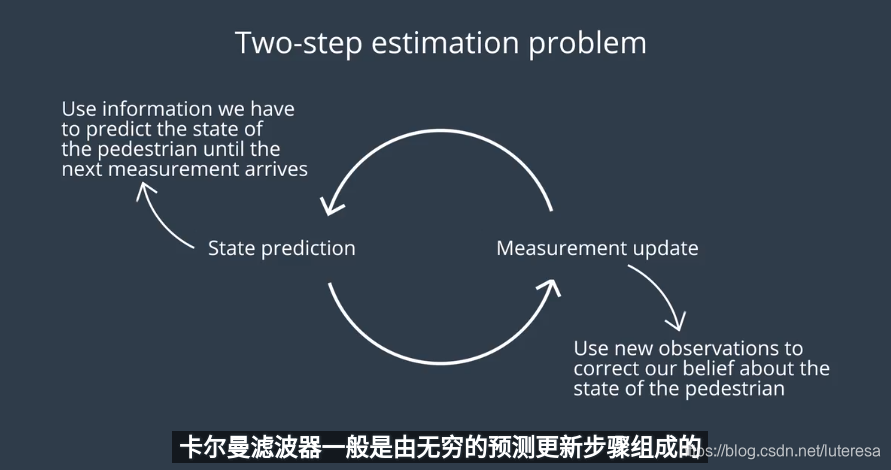
同样的,我们的卡尔曼滤波系统,还是由预测和测量两部分组成;
状态转移函数与之前完全一样
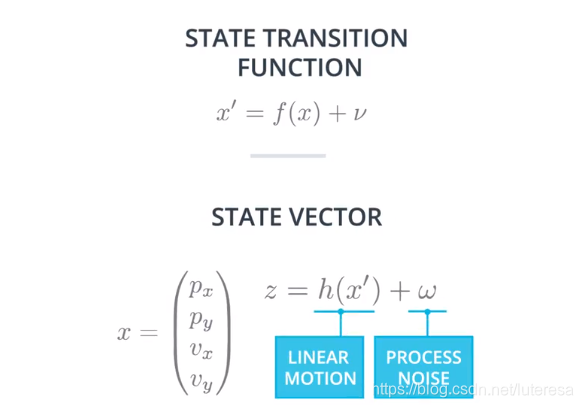
与之前单一传感器不同的是,现在需要融合多个传感器测量的数据,更新卡尔曼公式,系统关键部分如下图:
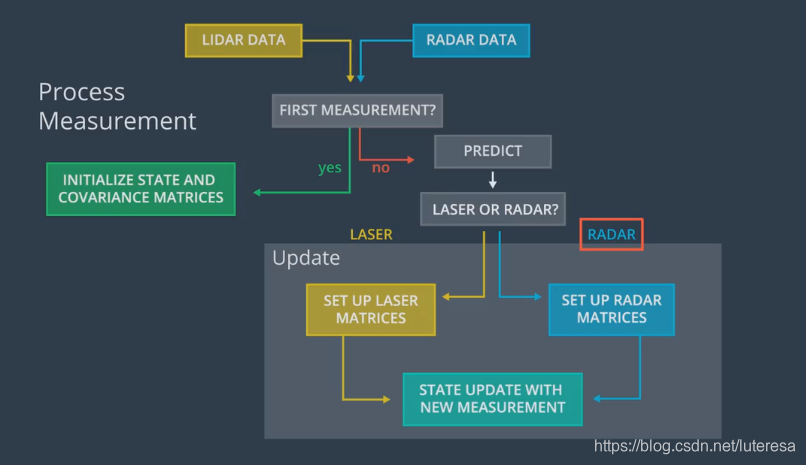
多传感器融合的原理是:任何一个传感器测量数据更新,都将引起行人状态的更新;
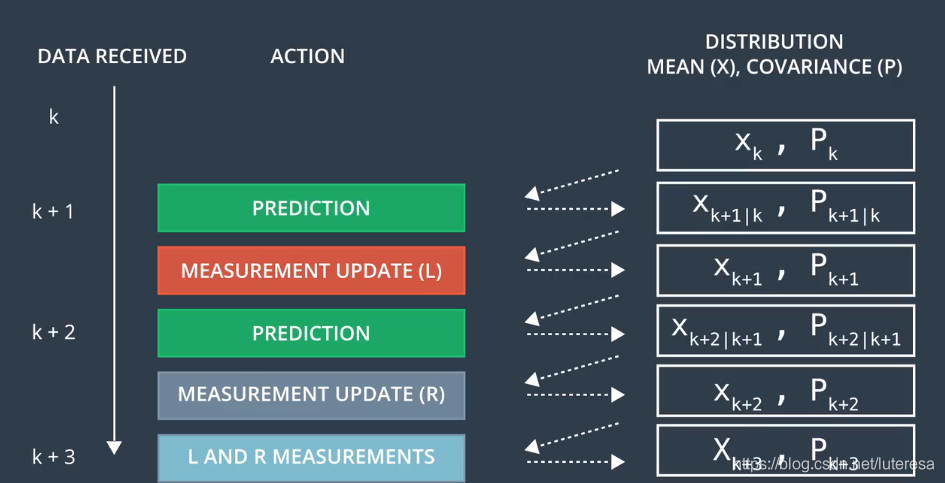
不同传感器都有自己固有属性,因此需要分别设计合适的测量转换矩阵(函数)
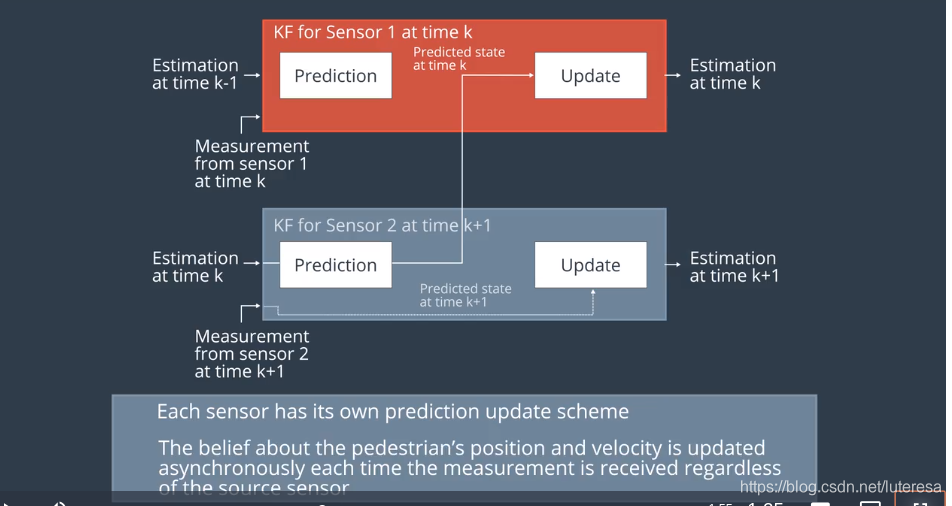
注意:当激光和雷达同时更新测量值时,只需要做一次预测更新。
2.1 激光测量转换函数
激光测量函数为
$$
H_L=
\left[\begin{matrix}
1&0&0&0\
0&1&0&0 \
\end{matrix}
\right]
$$
参考上一节卡尔曼滤波原理
https://blog.csdn.net/luteresa/article/details/104226258
2.2 雷达传感器
雷达传感器测量值包括:(无人车为原点,正前方为x方向,往左为y方向)
距离$\rho$:从原点(无人车)到行人的径向距离;
方向角$\varphi$: 射线L(从原点指向行人)与x轴的夹角;
径向速度$\dot{\rho}$: 沿射线L方向的速度

2.2.1 对h(x)函数进行线性化操作
考虑到测量向量的三个分量相互独立,它们的雷达测量协方差矩阵是一个3x3的对角线矩阵。
而我们的行人状态仍然是四个参数 $x = (p_x,p_y,v_x, v_y)^T$ ,测量向量有三个参数$(\rho, \varphi, \dot{\rho})^T$
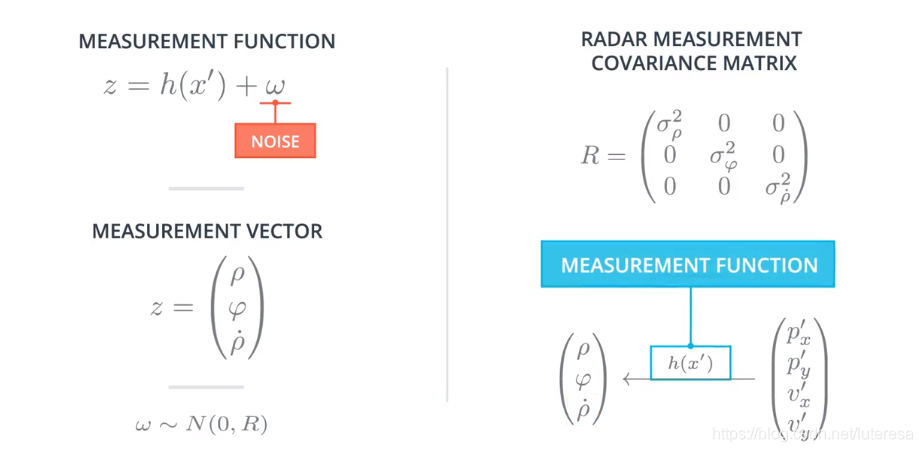
那么要把预测的状态$x^{'}$映射到测量空间,设计测量函数H如下:
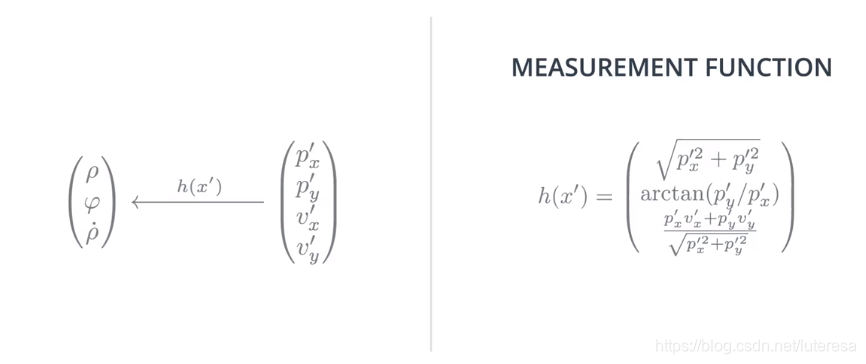
那么现在有以下问题:
问题1: 映射函数怎么得到的?
距离函数很简单,
$$
\rho = \sqrt{p_x^2 + p_y^2}
$$
夹角:
$$
\varphi = arctan(p_y/p_x)
$$
径向速度变化率:
方法1:微分方程

方法2:向量投影

问题2:转换矩阵中出现非线性函数时,有什么影响?
$$
\left[\begin{matrix}
\rho\
\varphi\
\dot{\rho} \
\end{matrix}
\right]=
\left[\begin{matrix}
\sqrt{p_x^2 + p_y^2}\
arctan(p_y/p_x)\
\frac{p_xv_x + p_yv_y}{\sqrt{p_x^2 + p_y^2}} \
\end{matrix}
\right]
$$
上面矩阵中的函数,是非线性函数。
假设使用高斯分布描述预测状态x,如果把这个高斯函数映射到非线性函数h(比如反正切),结果就不再是高斯分布了(如下图所示)。
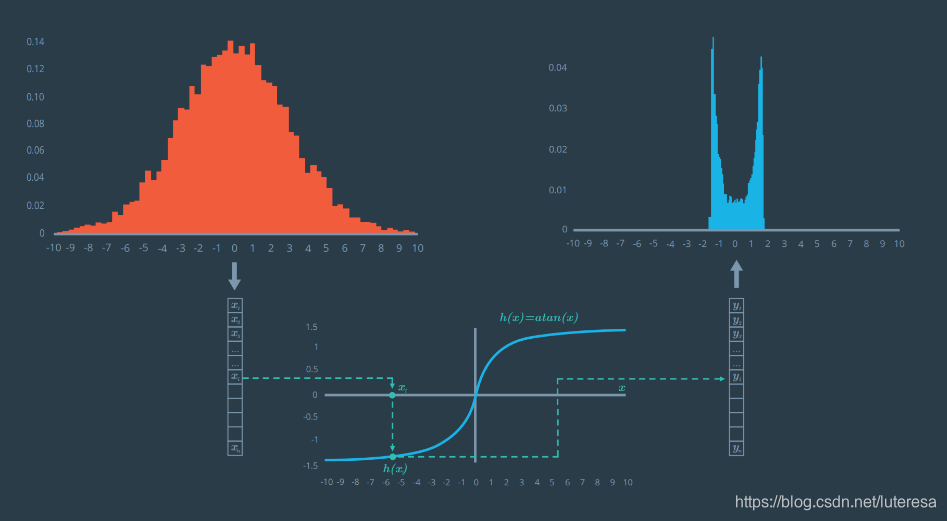
所以卡尔曼滤波不再适用。
为了解决这个问题,一个可行方案是对h(x)函数进行线性化操作,这就是==扩展卡尔曼滤波的核心思想==。
使用在原始高斯分布的均值位置,和h相切的一个线性函数,近似出测量值函数,重复上面同样的测试;
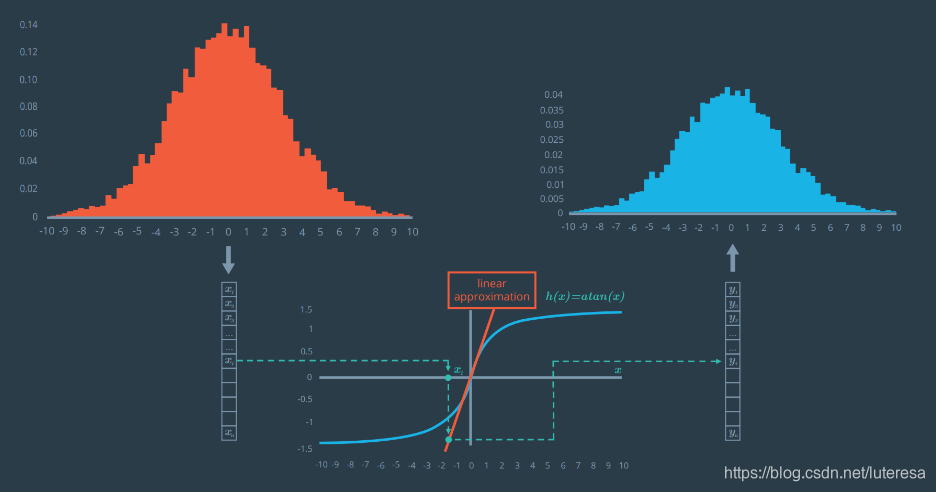
使用正太分布的同一个随机抽样值列表,改用h的近似传递所有$x_i$值,现在结果又呈现出高斯分布特征。
问题3:那么,如何对非线性函数进行线性化处理呢?
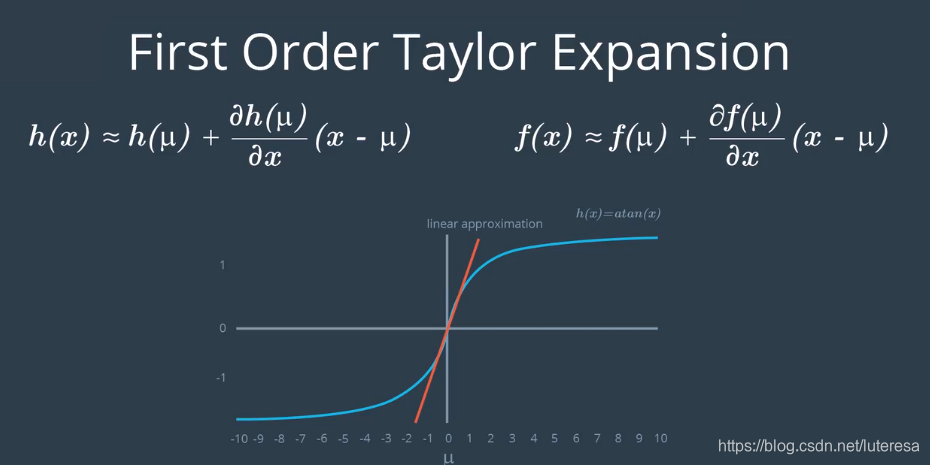
==扩展卡尔曼滤波器EKF==使用了一阶泰勒展开式,首先评估在均值位置$\mu$的非线性函数,这也是预测分布的最佳估算,然后使用围绕$\mu$的协度来推断这条线,斜率由h的第一个导数给出。
类似地,当状态转换f(x)也是非线性时,EKF采用完全一样的线性化转换。
2.2.2 雅可比式
如果把前面线性化例子归纳到更高的维度,那么函数h(x)对应于x的导数被称作雅可比式,它是一个3x4矩阵,包含所有偏导数:

雅可比矩阵是
$$
Hj=
\left[\begin{matrix}
\frac{p_x}{\sqrt{p_x^2 + p_y^2}} &\frac{p_y}{\sqrt{p_x^2 + p_y^2}}&0 &0\
-\frac{p_y}{p_x^2 + p_y^2}& -\frac{p_x}{p_x^2 + p_y^2}&0&0\
\frac{p_y(v_xp_y-v_yp_x)}{({p_x^2 + p_y^2})^{\frac{3}{2}}} &\frac{p_x(v_yp_x-v_xp_y)}{({p_x^2 + p_y^2})^{\frac{3}{2}}}& \frac{p_x}{\sqrt{p_x^2 + p_y^2}}&\frac{p_y}{\sqrt{p_x^2 + p_y^2}}\
\end{matrix}
\right]
$$
计算过程:
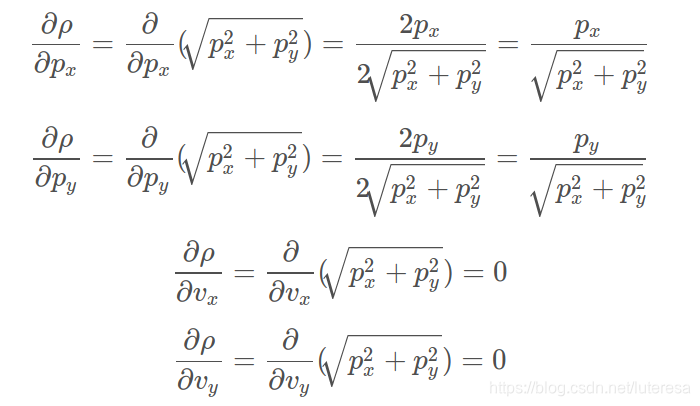
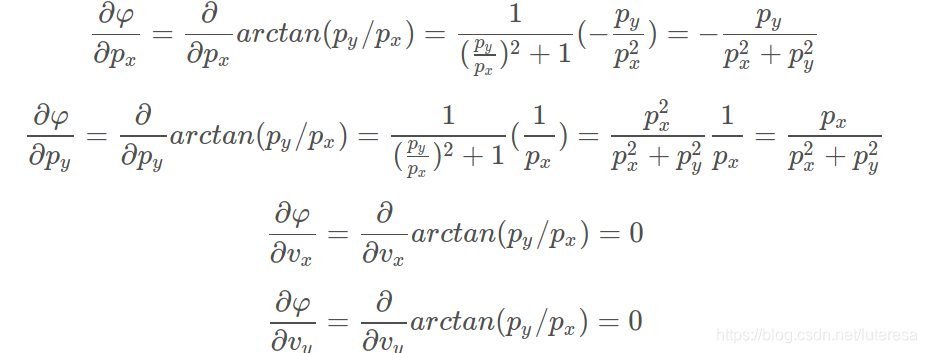

雅可比式C++实现:
#include <iostream>
#include <vector>
#include "Dense"
using Eigen::MatrixXd;
using Eigen::VectorXd;
using std::cout;
using std::endl;
MatrixXd CalculateJacobian(const VectorXd& x_state);
int main() {
/**
* Compute the Jacobian Matrix
*/
// predicted state example
// px = 1, py = 2, vx = 0.2, vy = 0.4
VectorXd x_predicted(4);
x_predicted << 1, 2, 0.2, 0.4;
MatrixXd Hj = CalculateJacobian(x_predicted);
cout << "Hj:" << endl << Hj << endl;
return 0;
}
MatrixXd CalculateJacobian(const VectorXd& x_state) {
MatrixXd Hj(3,4);
// recover state parameters
float px = x_state(0);
float py = x_state(1);
float vx = x_state(2);
float vy = x_state(3);
// pre-compute a set of terms to avoid repeated calculation
float c1 = px*px+py*py;
float c2 = sqrt(c1);
float c3 = (c1*c2);
// check division by zero
if (fabs(c1) < 0.0001) {
cout << "CalculateJacobian () - Error - Division by Zero" << endl;
return Hj;
}
// compute the Jacobian matrix
Hj << (px/c2), (py/c2), 0, 0,
-(py/c1), (px/c1), 0, 0,
py*(vx*py - vy*px)/c3, px*(px*vy - py*vx)/c3, px/c2, py/c2;
return Hj;
}3 扩展卡尔曼滤波器实现
相比线性系统,这里只是使用非线性函数f(x)来预测状态,使用h(x)计算测量误差,状态转换矩阵F和测量矩阵H被对应的雅可比式F、H和$H_j$替代

ps:当传感器属性是线性系统时,扩展卡尔曼滤波与卡尔曼滤波完全相同。
现在回到最初的流程图
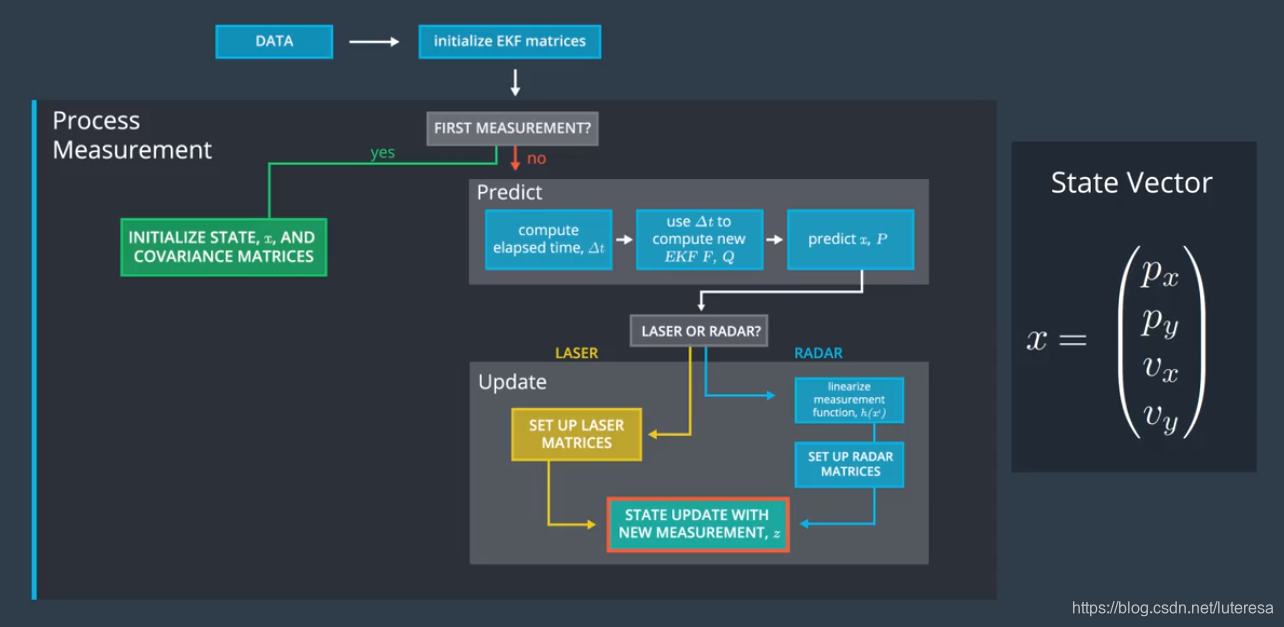
算法过程:
跟踪一名行人,他的状态通过二维位置向量和二维速度向量表示,$x = (p_x,p_y,v_x, v_y)^T$ ,每次收到来自特定传感器的新测量值时,都会触发估算函数process measurement,
第一次迭代时,仅初始化状态向量和协方差矩阵;
随后调用了预测和测量更新,在预测前,我们必须计算当前和前一次观察之间的时间差,根据时间差,我们计算新的状态转换,和过程协方差矩阵;
测量更新步骤取决于传感器类型,因此如果当前观察数据来自雷达传感器,必须计算新的雅可比矩阵$H_j$,使用非线性测量函数来估算预测状态并调用测量更新;
否则,如果当前观察数据来自激光雷达,那么只需使用激光雷达的H和R矩阵设置扩展卡尔曼滤波,让那后调用测量更新。
4.算法评估
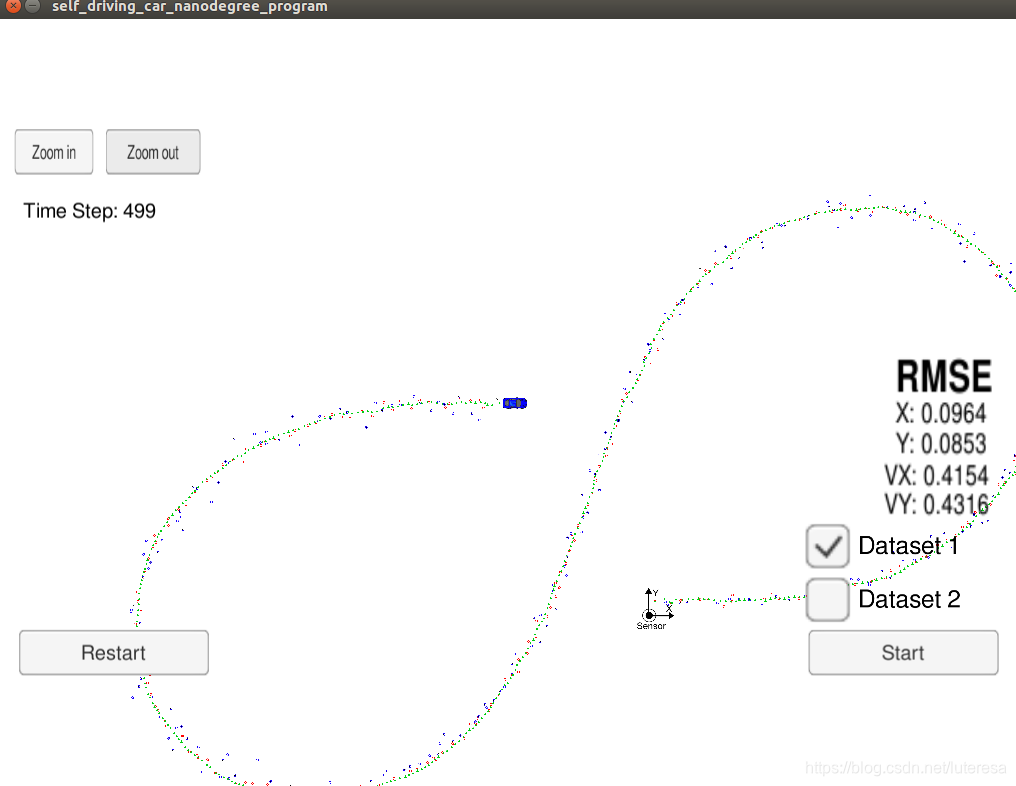
当我们实现了追踪算法之后,我们需要检查算法效果如何,评估估算结果和真实结果差别有多大;有很多评估标准,但最常见的标准叫做均方根误差。

在追踪场景下,它是一个准确度标准,可测量估算状态和真实状态之间的偏差。
它需要两个分量:
估算状态:这是一个向量,带有位置和速度分量;
真实数值:通常叫做标定的真实数值;
估算状态和真实状态之间的差,叫做==残差==,这些残差先平方然后求均值,最后得到平方根就是误差。
误差越低,估算准确率就越高。
C++实现:
#include <iostream>
#include <vector>
#include "Dense"
using Eigen::MatrixXd;
using Eigen::VectorXd;
using std::cout;
using std::endl;
using std::vector;
VectorXd CalculateRMSE(const vector<VectorXd> &estimations,
const vector<VectorXd> &ground_truth);
int main() {
/**
* Compute RMSE
*/
vector<VectorXd> estimations;
vector<VectorXd> ground_truth;
// the input list of estimations
VectorXd e(4);
e << 1, 1, 0.2, 0.1;
estimations.push_back(e);
e << 2, 2, 0.3, 0.2;
estimations.push_back(e);
e << 3, 3, 0.4, 0.3;
estimations.push_back(e);
// the corresponding list of ground truth values
VectorXd g(4);
g << 1.1, 1.1, 0.3, 0.2;
ground_truth.push_back(g);
g << 2.1, 2.1, 0.4, 0.3;
ground_truth.push_back(g);
g << 3.1, 3.1, 0.5, 0.4;
ground_truth.push_back(g);
// call the CalculateRMSE and print out the result
cout << CalculateRMSE(estimations, ground_truth) << endl;
return 0;
}
VectorXd CalculateRMSE(const vector<VectorXd> &estimations,
const vector<VectorXd> &ground_truth) {
VectorXd rmse(4);
rmse << 0,0,0,0;
// TODO: YOUR CODE HERE
// check the validity of the following inputs:
// * the estimation vector size should not be zero
// * the estimation vector size should equal ground truth vector size
if (estimations.size() != ground_truth.size()
|| estimations.size() == 0) {
std::cout << "Invalid estimation or ground_truth data" << std::endl;
return rmse;
}
// TODO: accumulate squared residuals
for (int i=0; i < estimations.size(); ++i) {
// ... your code here
VectorXd residual = estimations[i] - ground_truth[i];
// coefficient-wise multiplication
residual = residual.array()*residual.array();
rmse += residual;
}
// TODO: calculate the mean
rmse = rmse/estimations.size();
// TODO: calculate the squared root
rmse = rmse.array().sqrt();
// return the result
return rmse;
}5. 传感器融合项目实例
一个C++实现的完整扩展卡尔曼滤波实例,也是优达学城的无人驾驶纳米课程第五个项目;
项目代码:
https://github.com/luteresa/P5-Extended-Kalman-Filter
运行结果: