支持向量机(support vector machines)
优点:泛化错误率低,计算开销不大,结果易解释
缺点: 对参数调节和核函数的选择敏感,原始分类器不加修改仅适用于处理二分类问题。
适用数据类型: 数值型和标称型数据。
是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。
由简至繁的模型包括:
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机
支持向量,距离最大化:
距离分类超平面最近的点(支持向量),点到超平面距离越大,分类更优;

误差最小化
度量模型,一种是看误分类多少点(分类误差),一种是看间隔多宽(边际误差),
margin最大化,误差越小
边际误差计算
首先,$W = (w_1, w_2),x = (x_1,x_2), 并且 Wx = w_1x_1 + w_2x_2$
请注意,在这里我们有三条线,方程如下:(这里取“+/-1”,是基于计算方便考虑, 相对逻辑回归的0/1)
Wx+b=1
Wx+b=0
Wx+b=-1
该向量与方程为 Wx=1的线条相交于蓝点。假设该点的坐标为 (p,q)。那么我们可以得到下面两个结果:
$w_1p + w_2q = 1$(由于该点位于这条线上),并且
由于该点位于向量 $W = (w_1, w_2)$上(p,q) 是 $(w_1, w_2)$的倍数。
我们可以这样求解这个方程:对于某个 k 值而言,有 $(p,q) = k(w_1, w_2)$
那么我们的第一个方程将被转换为 $k(w_1^2 + w_2^2) = 1$
因此,$k = \frac{1}{w_1^2+w_2^2} = \frac{1}{|W|^2}$。这也就是说,蓝点表示向量 $\frac{W}{|W|^2}$
如图所示。

最后,最终距离是这连续两条平行线之间的距离之和。由于每两条线之间的距离为$\frac{1}{|W|} ,那么总距离为 \frac{2}{|W|} 。$
误差函数
误差函数是分类误差和边际误差的总和,通过梯度下降法,最小化误差函数,

C参数
当数据不是100%线性可分时,有必要引入参数C;
常数C控制“最大化间隔”和“保证大部分点的函数间隔小于1.0的”的权重,根据不同的应用场景,有时需要更高的准确性,有时需要更好的泛化能力,这种灵活性,通过C参数来提供。

如果C较大,更关注数据的正确分类,而不是寻找更合适的间隔;
如果C较小,那大部分误差就是边际误差,此时更注重合适的间隔,而不是数据准确性;
注意: 当 C 值对一组特定数据太大时,你可能根本无法收敛,因为总会有些分类错误的点不能被成功分离。
我们看到了支持向量机的三种不同实现方法:
最大间隔分类器
线性不可分类型的分类
核方法
核方法
最后,我们学习核方法,它使支持向量机真正强大。支持向量机中的核方法,使我们能在线性不可分情况下分离数据。
具体来说,你看到了两种类型的核:
多项式
径向基函数 (rbf)
多项式核
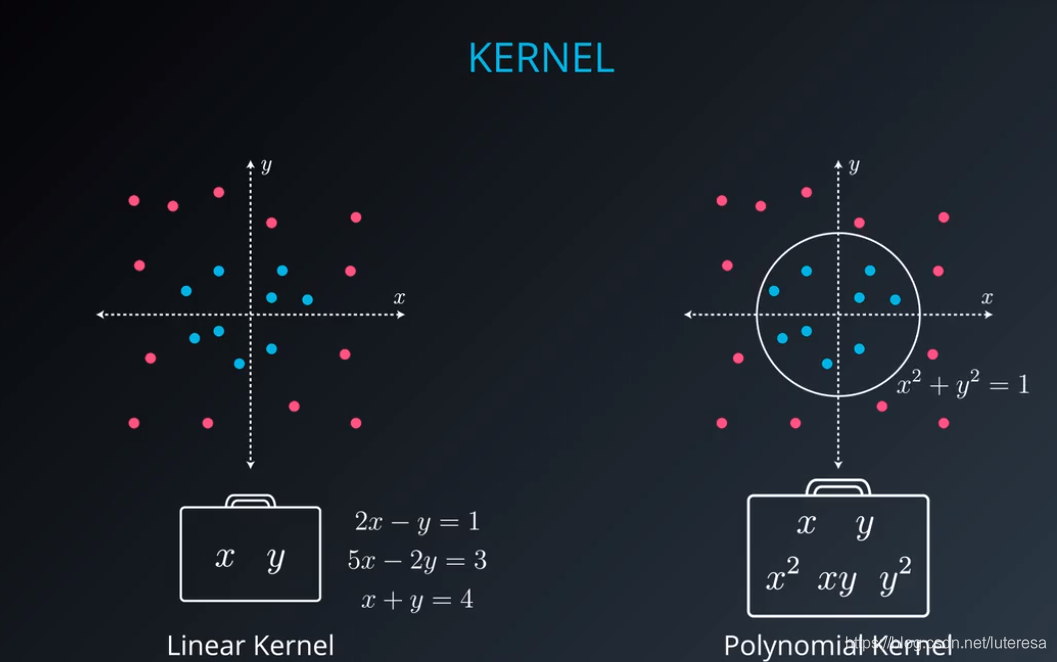
径向基函数 (rbf)
当前最流行的核是 rbf(径向基函数)。rbf 核使你有可能对在任何空间都难以分离的点进行分类。
一维
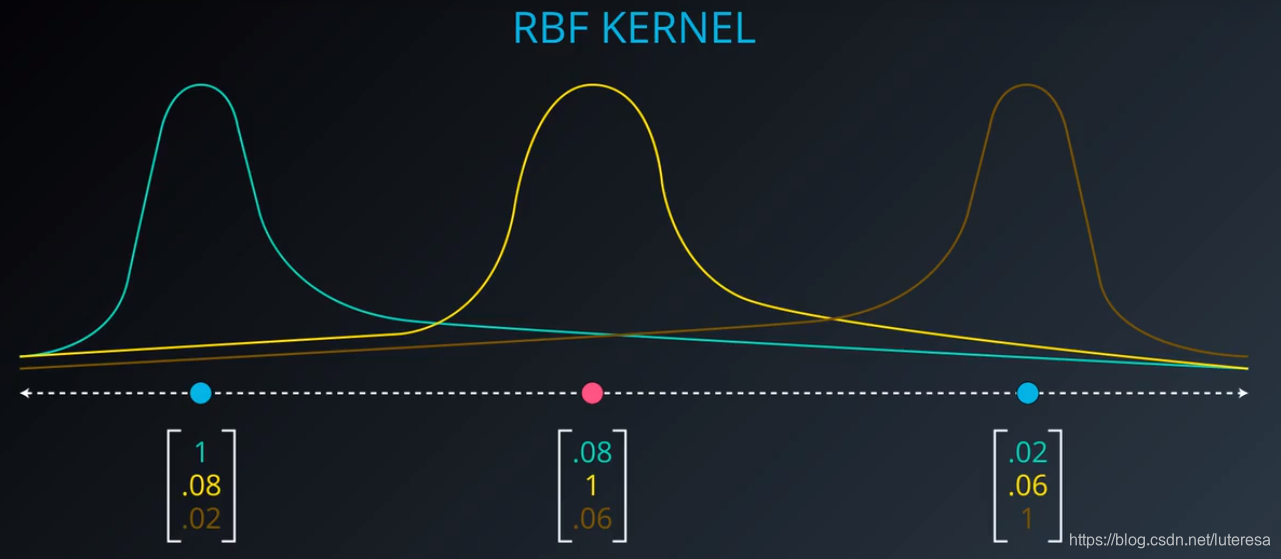
二维
也就是说对于原有数据集,添加一个维度,就可以分离任何空间;
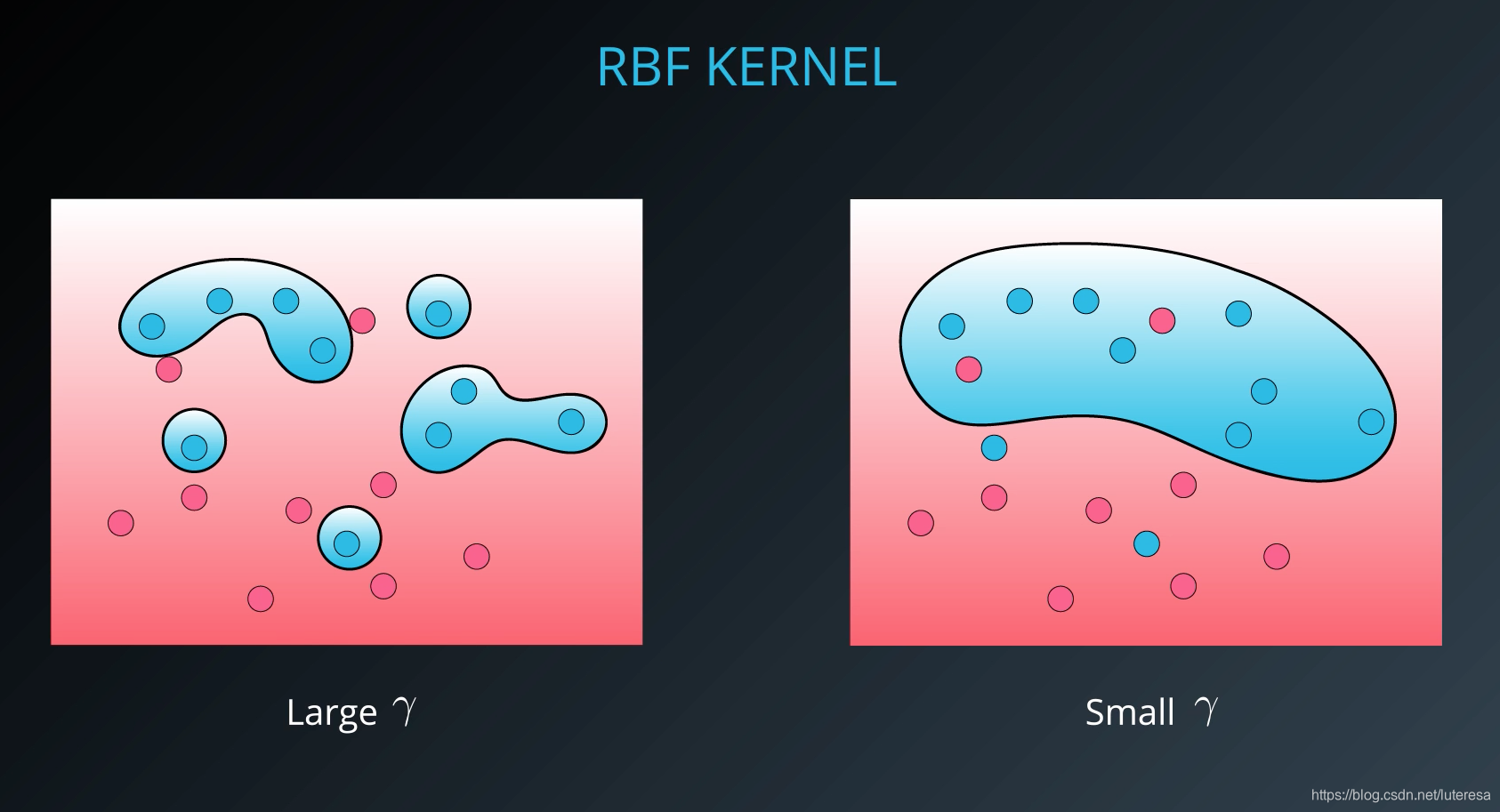
这是一种观察点间紧密程度的基于密度的方法。 这里引入另一个超参数 gamma。
当 gamma 取较大值时,其结果类似于C有较大值,即你的算法将尝试正确分类所有的点。于此相对,
当 gamma 较小时, 你的算法将尝试以更泛化方式进行分类,这样会增加分类错误,但会提高泛化能力。
sklearn中的支持向量机
# Import statements
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
import pandas as pd
import numpy as np# Read the data.
data = np.asarray(pd.read_csv('data.csv', header=None))
# Assign the features to the variable X, and the labels to the variable y.
X = data[:,0:2]
y = data[:,2]#加载模型
# TODO: Create the model and assign it to the variable model.
# Find the right parameters for this model to achieve 100% accuracy on the dataset.
model = SVC(kernel='rbf', gamma=30)
# TODO: Fit the model.
model.fit(X,y)SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma=30, kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)# TODO: Make predictions. Store them in the variable y_pred.
y_pred = model.predict(X)
# TODO: Calculate the accuracy and assign it to the variable acc.
acc = accuracy_score(y, y_pred)print(acc)1.0