1.错误类型
机器学习中常犯的两个错误是,过于简化模型,过于复杂化模型
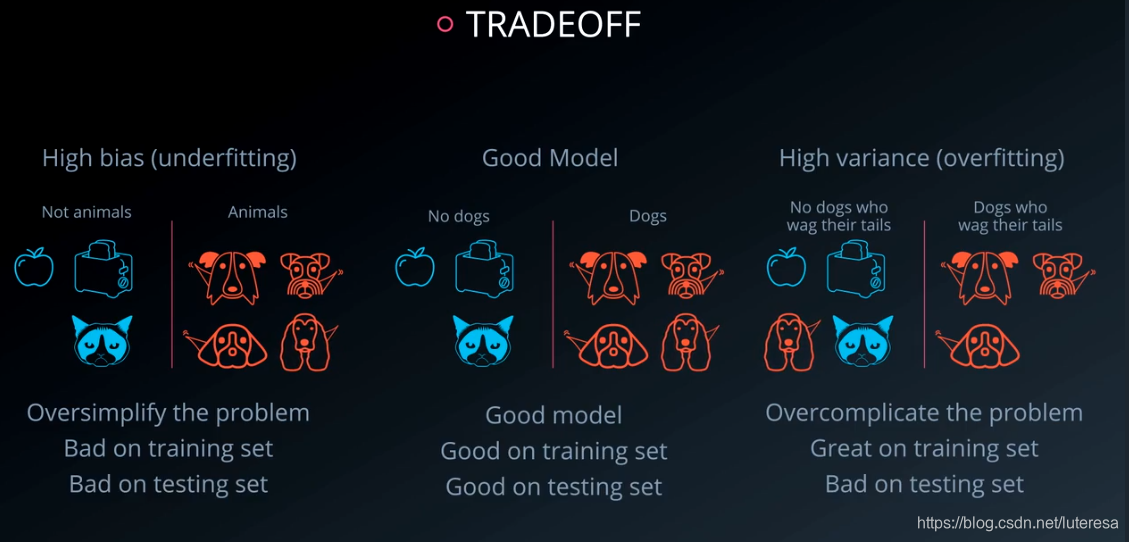
2.交叉验证
之前将数据分为训练集和测试集,判定模型效果,实际上犯了一个错误,将测试集参与了模型判定。
为更客观的反映模型效果,引入一个新的子集,交叉验证集。
一般复杂模型如下图,训练误差越来越小,测试误差开始很大,然后逐渐减小,然后再逐渐变大。
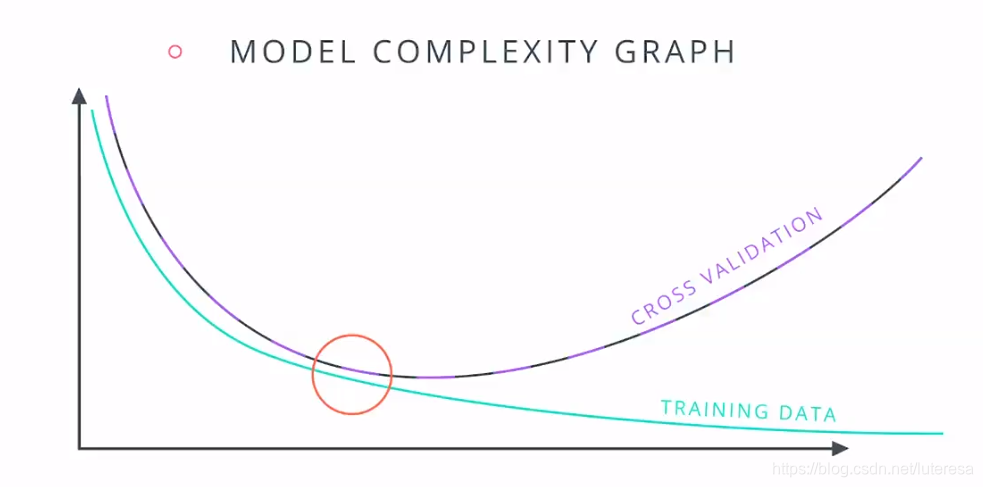
左侧欠拟合,右侧过拟合。
3. K 折交叉验证
将数据分成K份,然后训练模型K次,每次轮流取不同的几分数据作为测试集,剩余数据作为训练集,然后对结果取平均,得到最终的模型。
从SKLearn库中调用K折交叉验证很简单,创建一个K折交叉验证对象,其参数分别是数据的大小和测试集的大小,建议每次都随机化数据,以消除任何偏差暗示,

4.学习曲线
以训练数据样本数为横轴,误差为纵轴,画出训练集和交叉验证集的误差曲线
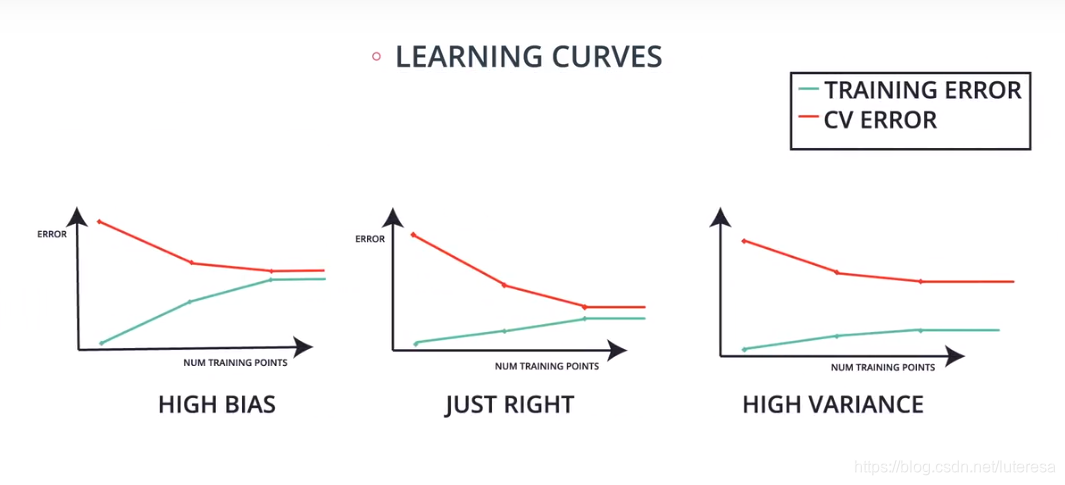
在高偏差或欠拟合模型中,两个曲线彼此逐渐靠近,收敛在高点;
好的模型中,两个曲线彼此逐渐靠近,并且收敛在低点;
在高方差或过拟合模型中,两个曲线不会彼此靠近,训练误差曲线保持在低位,而交叉验证误差曲线保持在高位;
这是区分欠拟合和过拟合的一种方法;
通过学习曲线检测过拟合和欠拟合实例
做个测验,我们将使用三个模型来训练下面的圆形数据集。
决策树模型,
逻辑回归模型,
支持向量机模型。
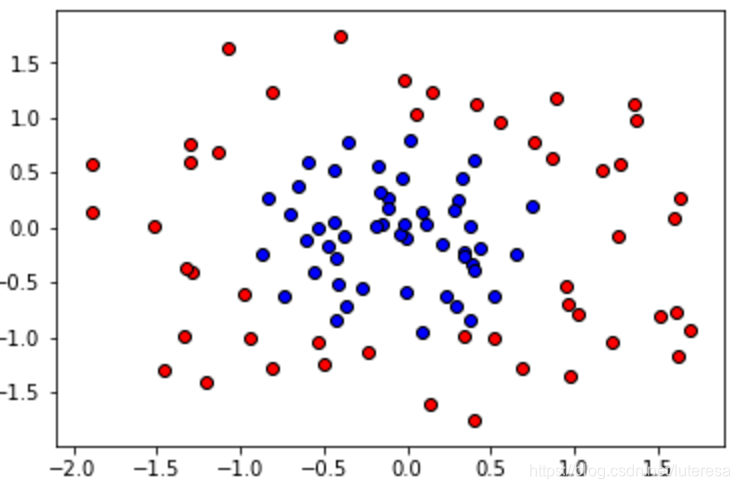
其中一个模型会过拟合,一个欠拟合,还有一个正常。首先,我们将编写代码为每个模型绘制学习曲线,最后我们将查看这些学习曲线,判断每个模型对应哪个曲线。
我们将使用函数 learning_curve:
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=None, n_jobs=1, train_sizes=np.linspace(.1, 1.0, num_trainings))
```
不需要担心该函数的所有参数([你可以在此处了解详情](https://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.html)),这里,我们将解释主要参数:
estimator,是我们针对数据使用的实际分类器,例如 LogisticRegression() 或 GradientBoostingClassifier()。
X 和 y 是我们的数据,分别表示特征和标签。
train_sizes 是用来在曲线上绘制每个点的数据大小。
train_scores 是针对每组数据进行训练后的算法训练得分。
test_scores 是针对每组数据进行训练后的算法测试得分。
## 两个重要的现象:
a.训练和测试得分是一个包含 3 个值的列表,这是因为函数使用了 3 折交叉验证。
b.**非常重要**:可以看出,我们使用训练和测试误差来定义我们的曲线,而这个函数使用训练和测试得分来定义曲线。二者是相反的,因此误差越高,得分就越低。因此,当你看到曲线时,你需要自己在脑中将它颠倒过来,以便与上面的曲线对比。
```python
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import learning_curve
# It is good to randomize the data before drawing Learning Curves
def randomize(X, Y):
permutation = np.random.permutation(Y.shape[0])
X2 = X[permutation,:]
Y2 = Y[permutation]
return X2, Y2
def draw_learning_curves(X, y, estimator, num_trainings,estimator_name):
train_sizes, train_scores, test_scores = learning_curve(
estimator, X2, y2, cv=None, n_jobs=1, train_sizes=np.linspace(.1, 1.0, num_trainings))
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.title("Learning Curves")
plt.xlabel("Training examples_"+estimator_name)
plt.ylabel("Score")
plt.plot(train_scores_mean, 'o-', color="g",
label="Training score")
plt.plot(test_scores_mean, 'o-', color="y",
label="Cross-validation score")
plt.legend(loc="best")
plt.savefig("./"+estimator_name+".png")
plt.show()# Import, read, and split data
import pandas as pd
data = pd.read_csv('data.csv')
import numpy as np
X = np.array(data[['x1', 'x2']])
y = np.array(data['y'])
# Fix random seed
np.random.seed(55)
### Imports
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.svm import SVC
# TODO: Uncomment one of the three classifiers, and hit "Test Run"
# to see the learning curve. Use these to answer the quiz below.
### Logistic Regression
#estimator = LogisticRegression()
#estimator_name = "LogisticRegression"
### Decision Tree
#estimator = GradientBoostingClassifier()
#estimator_name = "GradientBoostingClassifier"
### Support Vector Machine
estimator = SVC(kernel='rbf', gamma=1000)
estimator_name = "SVC"
num_trainings = len(y)/10
print(len(y),num_trainings)
X2, y2 = randomize(X, y)
draw_learning_curves( X, y,estimator,num_trainings,estimator_name)100 10.0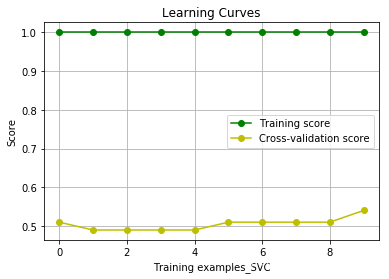
分别获得曲线:

我们可以根据这些曲线得出结论:
对数几率回归模型的训练和测试得分很低。
决策树模型的训练和测试得分很高。
支持向量机模型的训练得分很高,测试得分很低。
$\underline{由此可以判断,逻辑回归模型欠拟合,支持向量机模型过拟合,决策树正常}$。
同样,我们可以翻转这些曲线(因为它们测量的是得分,而原始曲线测量的是错误),并将它们与下面的三条曲线对比,可以看出它们与我们之前看到的三条曲线很像。(注意:我们需要翻转曲线并不意味着错误是 1 减去得分。只是表示模型越来越好的话,错误会降低,得分会升高。)
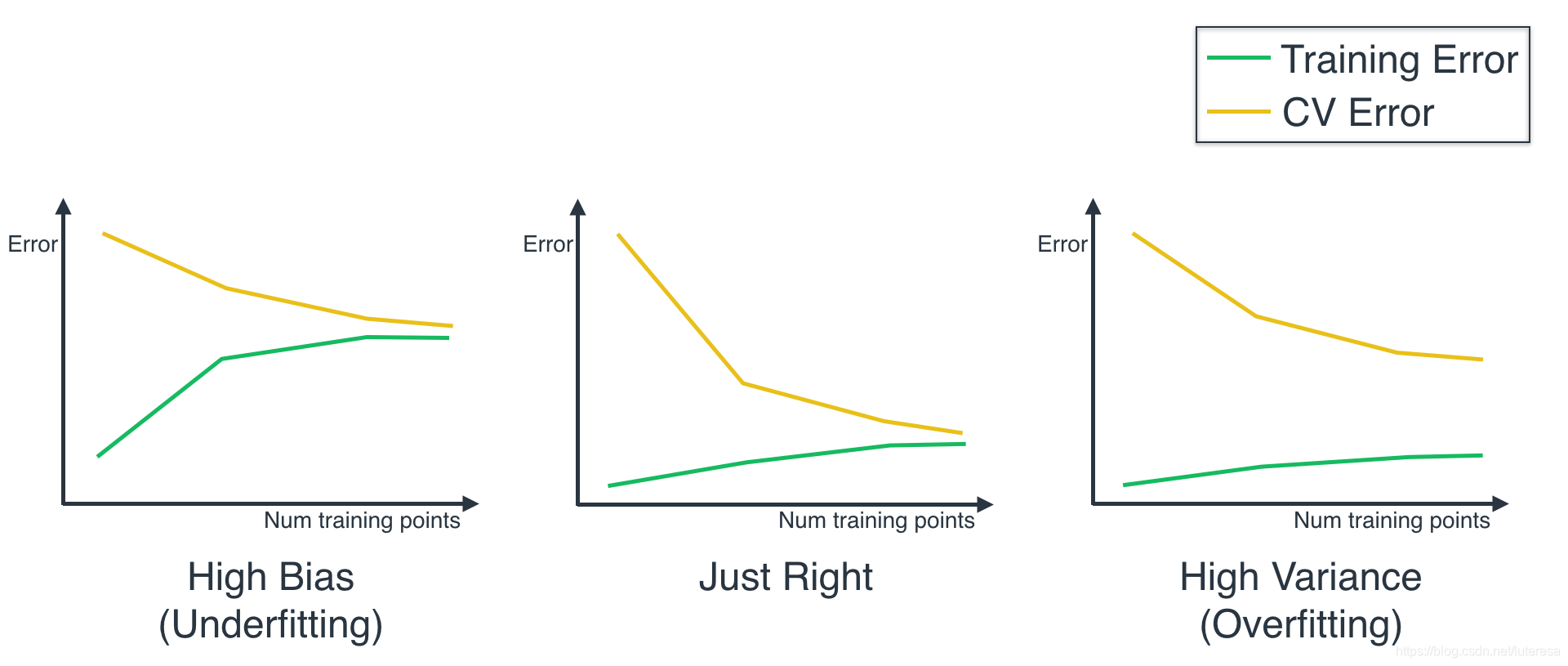
现在我们应该检测在实际模型中是否这样。当我们绘制每个模型的界限曲线时,结果如下所示:

当我们查看上述模型时,第一个模型欠拟合,第二个正常,第三个过拟合,这种现象合理吗?合理吧?我们看到数据由圆圈或方框正确地划分出来。我们的模型按以下形式划分数据:
逻辑回归模型使用一条直线,这太简单了。在训练集上的效果不太好,因此欠拟合。
决策树模型使用一个方形,拟合的很好,并能够泛化。因此,该模型效果很好。
支持向量机模型实际上在每个点周围都画了一个小圆圈。它实际上是在记住训练集,无法泛化。因此 过拟合。
最好尽可能进行实际检查,确保模型的确具有指标所指示的行为。
5.网格搜索
总结一下机器学习过程:
首先用训练集训练一些模型,然后利用交叉验证集数据在其中选择一个最好的模型,最后利用测试数据进行检测来保证这个模型是最好的。
这是一个训练逻辑回归的例子:
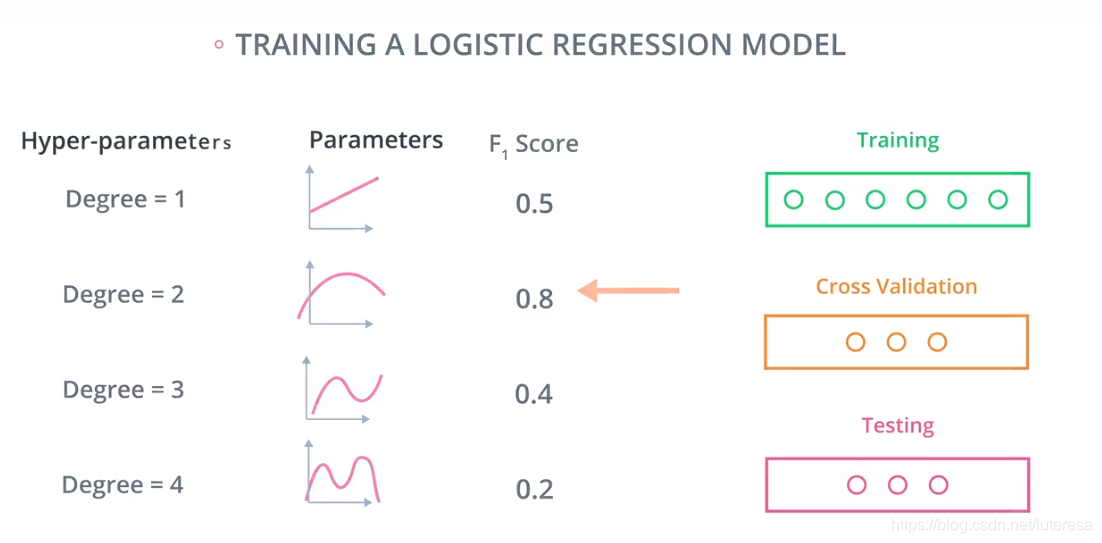
它是一条直线,一个二阶、三阶和四阶模型,用训练集数据来训练这个多项式的斜率和系数参数等,用交叉验证集数据来计算F1分数值
然后选择F1分数最高的模型,最后使用测试数据来确保所选模型是最好的.
同理,看另外一个例子,训练决策树,它的超参数是,深度
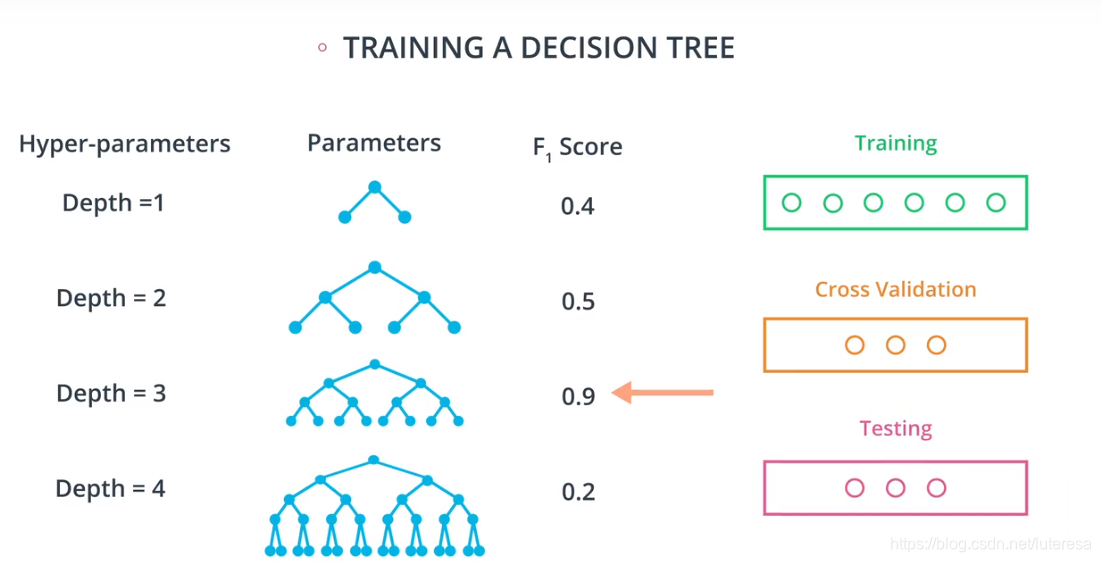
如果有多个超参数,比如训练支持向量机,如何在核参数和C参数之间选择最佳组合呢?
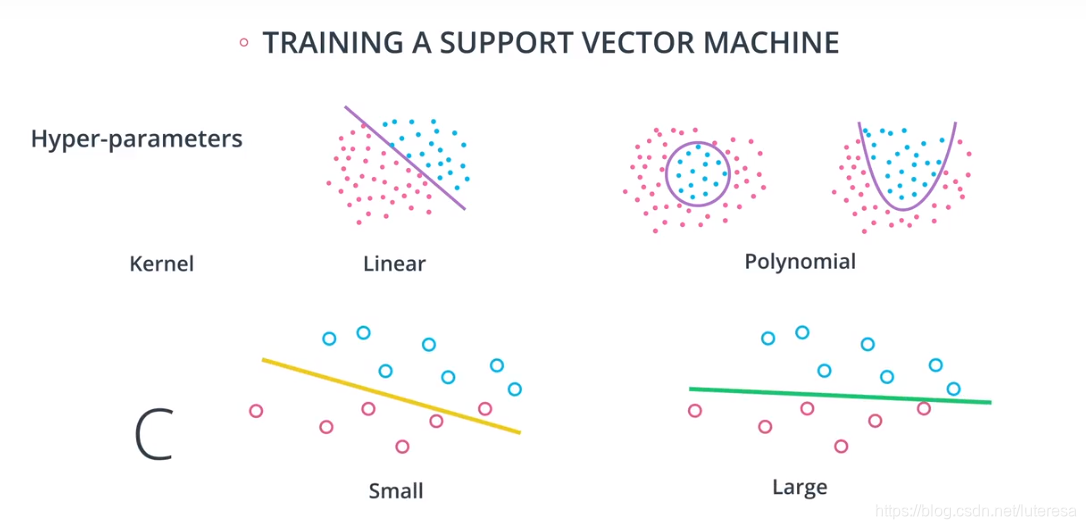
用网格搜索,做一张有各种可能性的表格,用训练集数据训练模型,然后用交叉验证集计算,选择F1分数最高值。
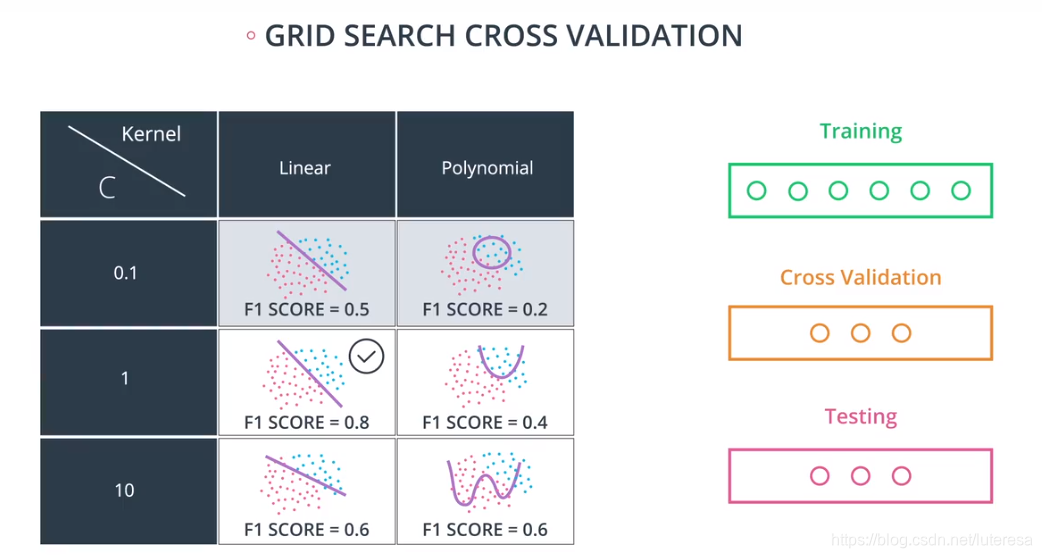
6.在sklearn中的网格搜索
假设我们想要训练支持向量机,并且我们想在以下参数之间做出决定:
kernel:poly或rbf。
C:0.1,1 或 10。
6.1 导入 GridSearchCV
from sklearn.model_selection import GridSearchCV6.2 选择参数:
现在我们来选择我们想要选择的参数,并形成一个字典。 在这本字典中,键 (keys) 将是参数的名称,值 (values) 将是每个参数可能值的列表。
parameters = {'kernel':['poly', 'rbf'],'C':[0.1, 1, 10]}6.3 创建一个评分机制 (scorer)
我们需要确认将使用什么指标来为每个候选模型评分。 这里,我们将使用 F1 分数。
from sklearn.metrics import make_scorer
from sklearn.metrics import f1_score
scorer = make_scorer(f1_score)6.4 使用参数 (parameter) 和评分机制 (scorer) 创建一个 GridSearch 对象。 使用此对象与数据保持一致 (fit the data) 。
# Create the object.
grid_obj = GridSearchCV(clf, parameters, scoring=scorer)
# Fit the data
grid_fit = grid_obj.fit(X, y)6.5 获得最佳估算器 (estimator)
best_clf = grid_fit.best_estimator_现在可以使用这一估算器best_clf来做出预测。
实例参考